 |
 |
 |
|
|
 |
 |
|
 |
 |
 |
 |
|
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
|
| DURATA CORSO: |
3 dicembre 2004 - 12 febbraio 2005 |
| ORE COMPLESSIVE: |
52 |
| COSTO: |
Euro 200,00 + IVA |
| DATA APPELLO: |
14 febbraio 2005 |
| CALENDARIO (aggiornato al 22 gennaio 2005): |
| Giorno |
Luogo * |
Argomento |
| Venerdì |
3 dicembre 2004 |
17:00 - 20:00 |
|
Collegio |
Modulo 1 |
 |
 |
 |
| Sabato |
11 dicembre 2004 |
9:00 - 13:00 |
Lunedì |
13 dicembre 2004 |
17:00 - 20:00 |
| Sabato |
18 dicembre 2004 |
9:00 - 13:00 |
| Mercoledì |
22 dicembre 2004 |
17:00 - 20:00 |
| Lunedì |
10 gennaio 2005 |
17:00 - 20:00 |
|
|
Modulo 2 + 3 |
 |
 |
 |
| Sabato |
15 gennaio 2005 |
9:00 - 13:00 |
| Lunedì |
17 gennaio 2005 |
17:00 - 20:00 |
|
|
Modulo 4 |
 |
 |
 |
| Sabato |
22 gennaio 2005 |
9:00 - 13:00 |
| Lunedì |
24 gennaio 2005 |
17:00 - 20:00 |
|
|
Modulo 5 |
 |
 |
 |
| Sabato |
29 gennaio 2005 |
9:00 - 13:00 |
| Lunedì |
31 gennaio 2005 |
17:00 - 20:00 |
|
|
Modulo 6 |
 |
 |
 |
| Giovedì |
3 febbraio 2005 |
17:00 - 20:00 |
| Sabato |
5 febbraio 2005 |
9:00 - 13:00 |
| Lunedì |
7 febbraio 2005 |
17:00 - 20:00 |
| Sabato |
12 febbraio 2005 |
9:00 - 13:00 |
|
|
Esercizi e
ripasso |
 |
|
| * Cliccare sull'indicazione abbreviata della sede dove si terrà la lezione per visualizzarne i dettagli. |
| ** La lezione prevista per lunedì 13 dicembre è cancellata e verrà recuperata successivamente. |
| TESTI CONSIGLIATI: |
G. Monti – R. Pini, Lezioni di Matematica Generale: funzioni di variabile reale, LED.
L. Scaglianti, A.Torriero, Matematica : metodi ed applicazioni, CEDAM
M. Scovenna – R. Grassi, Matematica. Esercizi e temi d'esame, CEDAM
Appunti e dispense forniti dalle Docenti. |
| PROGRAMMA DEL CORSO (aggiornato al 4 febbraio 2005): |
| Modulo 1
Lo spazio reale 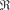 . Intervalli limitati e illimitati, intorno di un punto, massimo e minimo di un insieme, relazione tra punto e insieme. . Intervalli limitati e illimitati, intorno di un punto, massimo e minimo di un insieme, relazione tra punto e insieme.
|
| Modulo 2
Funzioni reali. Definizione di funzione; funzione suriettiva, iniettiva, biiettiva; esempi; funzioni monotone; funzione pari, dispari.
Trasformazioni di grafici: traslazioni, moduli; funzione limitata; massimi e minimi assoluti e relativi; funzione inversa. |
| Modulo 3
Limiti. Definizione di limite (in particolare definizione di lim ƒ(x) = l).
Esempi, operazioni sui limiti. Teorema di unicità del limite, teorema della permanenza del segno, teorema del confronto, teorema di esistenza del limite per funzioni monotone.
Limiti delle funzioni potenza, esponenziale e logaritmo, alcuni limiti notevoli, confronto tra potenze, esponenziali e logaritmi, confronto tra
infinitesimi (opzionale), confronto tra infiniti, simbolo di rapporto infinitesimo. |
| Modulo 4
Continuità. Definizione di continuità in un punto.
Punti di discontinuità e loro classificazione.
Teorema di Wierestrass; dei valori intermedi e degli zeri.
Asintoti orizzontali, verticali e obliqui. |
| Modulo 5
Rapporto incrementale e derivata. Rapporto incrementale e suo significato geometrico; derivata di funzione in un punto e suo significato geometrico; equazione della retta tangente ad una curva in un punto; funzioni derivabili: derivata destra e sinistra; punto angoloso e cuspide; relazione tra derivabilità e continuità. |
| Modulo 6
Funzioni derivabili. Derivate di funzioni elementari, Operazioni sulle derivate, derivata della funzione composta (solo esempi), derivate di ordine superiore, teoremi fondamentali del calcolo differenziale: Teorema di Rolle, Teorema de
l'Hospital, teorema di Fermat, condizioni sufficienti per l'esistenza di massimi e
minimi relativi, concavità, convessità e punti di flesso, schema per lo studio di una
funzione. |
 |
 |
|
 |
|
|
 |
 |
 |
 |
 |
|
 |
|
 |
 |
|
|
 |
 |