 |
|
|
 |
|
| DURATA CORSO: |
3 dicembre 2004 - 12 febbraio 2005 |
| ORE COMPLESSIVE: |
52 |
| COSTO: |
Euro 200,00 + IVA (cliccare qui per le coordinate bancarie del bonifico) Per iscriversi è necessario compilare il modulo on-line (cliccare qui), dal quale è possibile anche prenotare il libro di testo al costo di 32,00 Euro, ed effettuare il bonifico bancario (es. Euro 240,00 più Euro 32,00 se si desidera un testo) inviandone copia al numero di fax 02 9014828. |
| DOCENTI: |
Silvana Stefani
Ilaria Foroni |
| DATA APPELLO: |
14 febbraio 2005 |
| CALENDARIO (aggiornato al 22 gennaio 2005): |
| Giorno |
Luogo * |
Argomento |
Docente |
| Venerdì |
3 dicembre 2004 |
17:00 - 20:00 |
|
Collegio |
Modulo 1 |
Stefani |
|
|
|
| Sabato |
11 dicembre 2004 |
9:00 - 13:00 |
Lunedì |
13 dicembre 2004 |
17:00 - 20:00 |
| Sabato |
18 dicembre 2004 |
9:00 - 13:00 |
| Mercoledì |
22 dicembre 2004 |
17:00 - 20:00 |
| Lunedì |
10 gennaio 2005 |
17:00 - 20:00 |
|
|
Modulo 2 + 3 |
Foroni |
|
|
|
| Sabato |
15 gennaio 2005 |
9:00 - 13:00 |
| Lunedì |
17 gennaio 2005 |
17:00 - 20:00 |
|
|
Modulo 4 |
Stefani |
|
|
|
| Sabato |
22 gennaio 2005 |
9:00 - 13:00 |
| Lunedì |
24 gennaio 2005 |
17:00 - 20:00 |
|
|
Modulo 5 |
Stefani |
|
|
|
| Sabato |
29 gennaio 2005 |
9:00 - 13:00 |
| Lunedì |
31 gennaio 2005 |
17:00 - 20:00 |
|
|
Modulo 6 |
Stefani |
|
|
|
| Giovedì |
3 febbraio 2005 |
17:00 - 20:00 |
| Sabato |
5 febbraio 2005 |
9:00 - 13:00 |
| Lunedì |
7 febbraio 2005 |
17:00 - 20:00 |
| Sabato |
12 febbraio 2005 |
9:00 - 13:00 |
|
da confermare |
Esercizi e
ripasso |
|
|
|
| Foroni |
| Stefani |
| Foroni |
| Foroni |
|
|
|
| * Cliccare sull'indicazione abbreviata della sede dove si terrà la lezione per visualizzarne i dettagli. |
| ** La lezione prevista per lunedì 13 dicembre è cancellata e verrà recuperata successivamente. |
| TESTI CONSIGLIATI: |
G. Monti – R. Pini, Lezioni di Matematica Generale: funzioni di variabile reale, LED.
L. Scaglianti, A.Torriero, Matematica : metodi ed applicazioni, CEDAM
M. Scovenna – R. Grassi, Matematica. Esercizi e temi d'esame, CEDAM
Appunti e dispense forniti dalle Docenti. |
| PROGRAMMA DEL CORSO: |
| Modulo 1
Topologia di 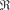 (punti di accumulazione, punti isolati, punti di frontiera). Insiemi aperti e insiemi chiusi, insiemi limitati. Estremo superiore e inferiore, massimo e minimo.
L'insieme dei numeri reali esteso: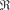 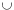{ 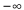}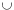{ 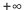}, definizione delle operazioni.
Funzione reale di variabile reale: definizione (dominio, insieme immagine). Funzione suriettiva, iniettiva, biunivoca. Grafico di una funzione. Funzioni monotòne, periodiche, pari e dispari. Estremo superiore e inferiore di una funzione, massimo e minimo assoluto e relativo di una funzione. Funzioni composte. Funzioni invertibili. |
| Modulo 2
Limiti di una funzione in un punto. Definizione. Teorema dell'unicità del limite. Teorema di permanenza del segno, di locale limitatezza. Algebra dei limiti. Cambiamento di variabile nel calcolo dei limiti. Forme di indecisione. Infinitesimi e infiniti e loro confronto. Simboli di Landau: o (o piccolo),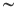 (asintotico). Limiti notevoli e applicazioni. |
| Modulo 3
Funzioni continue. La continuità delle funzioni elementari. Continuità delle funzioni composte. Teorema di Weierstrass, degli zeri e dei valori intermedi. Invertibilità e monotonia.
Punti di discontinuità e loro classificazione. Asintoti. Grafico di una funzione: primo approccio. |
| Modulo 4
Rapporto incrementale. Nozione di derivata, di derivata destra e sinistra.
Significato geometrico. Punti angolosi e cuspidi.
Relazione tra derivabilità e continuità (con dimostrazione). Derivate delle funzioni elementari. Regole di derivazione. Il Teorema di De l'Hôpital per la risoluzione di forme di indecisione. Derivata di funzione composta e inversa. Derivate di ordine superiore. |
| Modulo 5
Definizione di estremo relativo. Teorema di Fermat. Teoremi di Rolle e Lagrange. Conseguenze del Teorema di Lagrange. Ricerca dei punti di estremo relativo e assoluto. |
| Modulo 6
Formula di Taylor e Mc Laurin. Applicazioni della Formula di Taylor al calcolo dei limiti e alla determinazione di estremi relativi di funzioni derivabili.
Convessità e concavità: caratterizzazione per funzioni derivabili e derivabili due volte. Punti di flesso e studio di funzione.
|
|
|
|
|
